Flower

Andrea Giorgini


Zorn Postdoctoral Fellow
Department of Mathematics
Indiana University
agiorgin(at)iu(dot)edu
Flower

Research Interests
My research activity is focused on the study of nonlinear Partial Differential Equations arising from Fluid Mechanics, Biology and Materials Science. I am currently interested in modeling and theoretical analysis of Diffuse Interface (Phase Field) problems describing the evolution of two-phase fluid mixtures with complicated internal microstructures and driven by the surface tension.

My main research directions are:

  • Navier-Stokes-Cahn-Hilliard systems
  • Hele-Shaw and porous media flows with applications to tumor growth dynamics
  • Nonlocal models for long-range particle interactions
  • Multiphysics of complex fluids
    • Flower

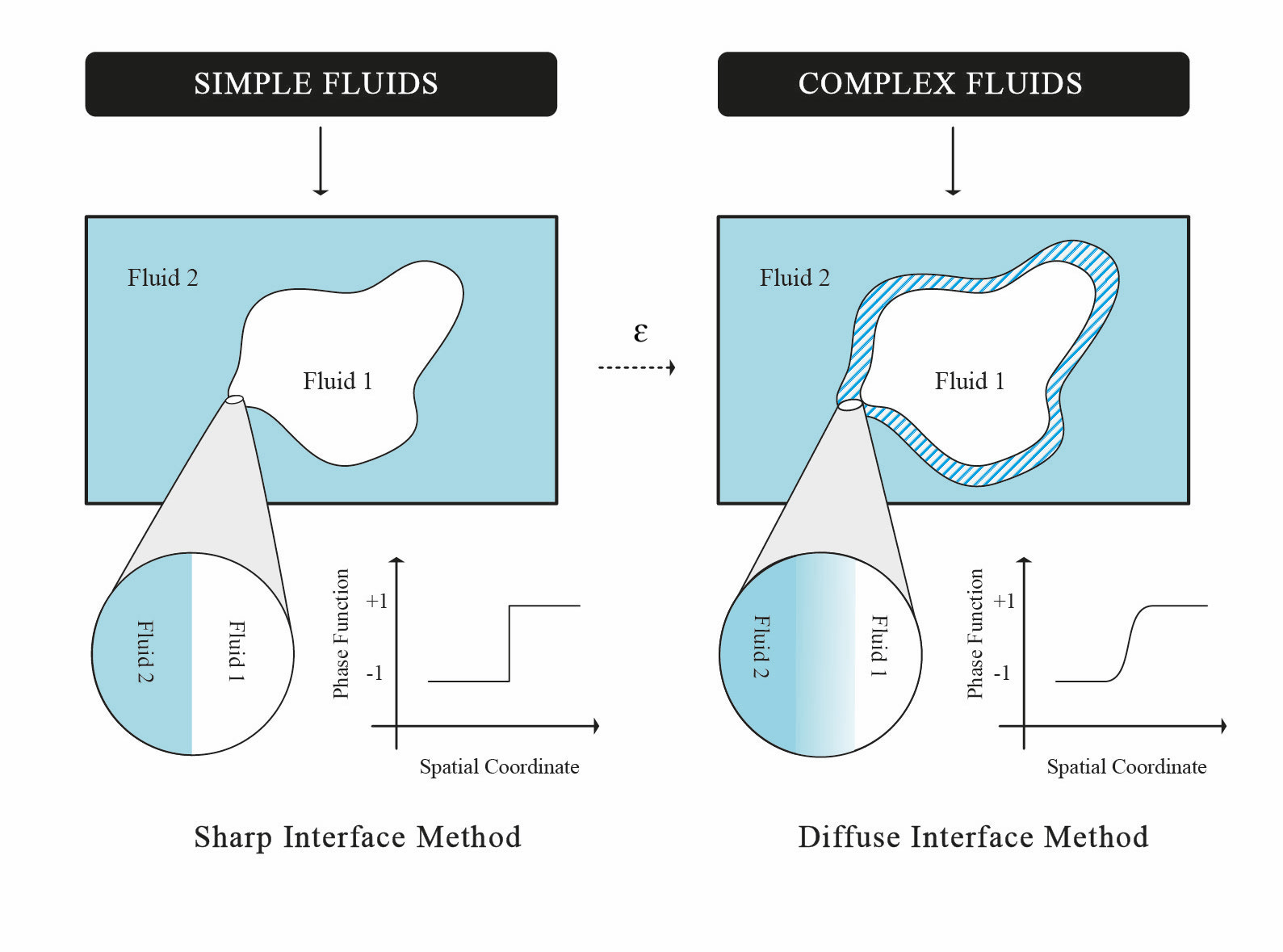
    Preprints

    • Continuous Data Assimilation for the 3D Ladyzhenskaya Model: Analysis and Computations
      Y. Cao, A. Giorgini, M. Jolly & A. Pakzad
      arXiv:2108.03513, 2021
    • On the existence of strong solutions to the Cahn-Hilliard-Darcy system with mass source
      A. Giorgini, K.F. Lam, E. Rocca & G. Schimperna
      arXiv:2009.13344, 2020
    • Diffuse interface models for incompressible binary fluids and the mass-conserving Allen-Cahn approximation
      A. Giorgini, M. Grasselli & H. Wu
      arXiv:2005.07236, 2020

    Publications

    1. Well-posedness of the two-dimensional Abels-Garcke-Grün model for two-phase flows with unmatched densities
      A. Giorgini
      Calculus of Variations and Partial Differential Equations 60, 100 (2021)
    2. The Navier-Stokes-Cahn-Hilliard equations for mildly compressible binary fluid mixtures
      A. Giorgini, R. Temam & X.-T. Vu
      Discrete & Continuous Dynamical Systems - B 26 (2021), 337-366. Special issue for the 20 years anniversary.
    3. Weak and strong solutions to the nonhomogeneous incompressible Navier-Stokes-Cahn-Hilliard system
      A. Giorgini & R. Temam
      Journal de Mathématiques Pure et Appliquées 144 (2020), 194-249
    4. Well-posedness of a diffuse interface model for Hele-Shaw flows
      A. Giorgini
      Journal of Mathematical Fluid Mechanics 22, 5 (2020)
    5. Well-posedness for the Brinkman-Cahn-Hilliard system with unmatched viscosities
      M. Conti & A. Giorgini
      Journal of Differential Equations 268 (2020), 6350-6384
    6. Uniqueness and regularity for the Navier-Stokes-Cahn-Hilliard system
      A. Giorgini, A. Miranville & R. Temam
      SIAM Journal on Mathematical Analysis 51 (2019), 2535-2574
    7. The nonlocal Cahn-Hilliard-Hele-Shaw system with logarithmic potential
      F. Della Porta, A. Giorgini & M. Grasselli
      Nonlinearity 31 (2018), 4851-4881
    8. The Cahn-Hilliard-Hele-Shaw system with singular potential
      A. Giorgini, M. Grasselli & H. Wu
      Annales de l'Institut Henry Poincaré C, Analyse Non Linéaire 35 (2018), 1079-1118
    9. Navier-Stokes-Voigt equations with memory in 3D lacking instantaneous kinematic viscosity
      F. Di Plinio, A. Giorgini, V. Pata & R. Temam
      Journal of Nonlinear Science 28 (2018), 653-686
    10. The nonlocal Cahn-Hilliard equation with singular potential: well-posedness, regularity and strict separation property
      C.G. Gal, A. Giorgini & M. Grasselli
      Journal of Differential Equations 263 (2017), 5253-5297
    11. The Cahn-Hilliard-Oono equation with singular potential
      A. Giorgini, M. Grasselli & A. Miranville
      Mathematical Models and Methods in Applied Sciences 27 (2017), 2485-2510
    12. Phase-field crystal equation with memory
      M. Conti, A. Giorgini & M. Grasselli
      Journal of Mathematical Analysis and Applications 436 (2016), 1297-1331
    13. On the Swift-Hohenberg equation with slow and fast dynamics: well-posedness and long-time behavior
      A. Giorgini
      Communications on Pure and Applied Analysis 15 (2016), 219-241

    Teaching

  • Spring 2021: Indiana University, M301 - Linear Algebra and Applications
  • Spring 2021: Indiana University, M119 - Brief Survey of Calculus 1
  • Fall 2020: Indiana University, M441 - Introduction to Partial Differential Equations with Applications 1
  • Spring 2020: Indiana University, M343 - Introduction to Differential Equations with Applications 1 (two sections)
  • Fall 2019: Indiana University, M441 - Introduction to Partial Differential Equations with Applications 1
  • Spring 2019: Indiana University, M365 - Introduction to Probability and Statistics
  • Fall 2018: Indiana University, M343 - Introduction to Differential Equations with Applications 1 (two sections)